Πως η αβεβαιότητα στην ενέργεια ενός σωματιδίου προσδιορίζει με εξαιρετική ακρίβεια τον χρόνο ζωής ασταθών σωματιδίων
Υπάρχουν σωματίδια που ζουν αιώνια ή για να το πούμε διαφορετικά, ο χρόνος ζωής τους είναι μεγαλύτερος από την ηλικία του σύμπαντος, όπως για παράδειγμα τα πρωτόνια, τα ηλεκτρόνια, τα νετρίνα και τα φωτόνια. Όμως, υπάρχουν και σωματίδια τα οποία όπως και οι άνθρωποι, έχουν πεπερασμένο χρόνο ζωής. Πολλά από αυτά πεθαίνουν σχεδόν αμέσως αφού παραχθούν. Για παράδειγμα, ένα ελεύθερο νετρόνιο ζεί περίπου 15 λεπτά, ένα μιόνιο 2,2 εκατομμυριοστά του δευτερολέπτου, το διάσημο σωματίδιο Higgs ζει λιγότερο από ένα τρισεκατομμυριοστό του δισεκατομμυριοστού του δευτερολέπτου ή 1,6×10-22 δευτερόλεπτα, ενώ τα μποζόνια W+, W− και Z0 ζουν ακόμα λιγότερο, γύρω στα 10−25 δευτερόλεπτα.
Ένας αναπάντεχος τρόπος για να υπολογίσουμε τον χρόνο ζωής των ασταθών σωματιδίων είναι διαμέσου της κβαντομηχανικής σχέσης: $\Delta E \cdot \Delta t \geq \dfrac{\hbar}{2}$. Η σχέση αυτή αποκαλείται συχνά "σχέση αβεβαιότητας ενέργειας-χρόνου", ένα παραπλανητικό όνομα, διότι ανακαλεί αδόκιμα την θεμελιώδη κβαντομηχανική σχέση αβεβαιότητας θέσης-ορμής $ \Delta p \cdot \Delta t \geq \dfrac{\hbar}{2}$. Όμως, η σύγκριση είναι άστοχη, εφόσον ο χρόνος δεν είναι παρατηρήσιμο μέγεθος προσαρτημένο σε ένα σωματίδιο. Το νόημα της σχέσης αυτής εξαρτάται από το είδος της μέτρησης που μας ενδιαφέρει. Μια πιο σωστή γραφή της σχέσης αυτής θα ήταν $ \Delta E \cdot T \geq \dfrac{\hbar}{2}$ , όπου το Τ συμβολίζει τον χαρακτηριστικό χρόνο μέσα στον οποίο η ενέργεια του κβαντικού συστήματος αλλάζει αξιόλογα.
Παραδείγματος χάριν, για ένα άτομο στη θεμελιώδη κατάσταση, το Τ είναι απεριόριστα μεγάλο και η ενέργεια προσδιορίσιμη σχεδόν με όση ακρίβεια θέλουμε. Όπως ακριβώς και με σωματίδια όπως τα πρωτόνια και τα ηλεκτρόνια, που έχουν μέση διάρκεια ζωής πρακτικά άπειρη και διαθέτουμε όλο το χρόνο για να εκτελέσουμε άμεσα αναρίθμητες μετρήσεις της μάζας τους (ισοδύναμα, της ενέργειας E=mc2) και να προκυψουν τιμές με εξαιρετική ακρίβεια. Η απροσδιοριστία στην ενέργεια (μάζα) που προέρχεται από την σχέση του Heisenberg θα φαίνεται αμελητέα.
Αν αντίθετα πρόκειται για ασταθή σωματίδια με πολύ σύντομη μέση διάρκεια ζωής, η μάζα (ενέργεια) τους δεν μπορεί να μετρηθεί άμεσα, διότι ο χρόνος που διαθέτουμε είναι πολύ περιορισμένος. Μπορούμε ωστόσο να μετρήσουμε την ενέργεια των προϊόντων διάσπασης και να βρούμε έτσι τη μάζα του μητρικού σωματιδίου. Το αξιοπρόσεκτο είναι ότι, ακόμα κι αν είχαμε απεριόριστη πειραματική ακρίβεια, κάθε μέτρηση θα έδινε ελαφρώς διαφορετικά αποτελέσματα. Δεν πρέπει να ξεχνάμε ότι στους απειροελάχιστους χρόνους της σύντομης ζωής του αυτό που 'ταλαντώνεται' είναι η ενέργεια του μητρικού σωματιδίου.
Μια καμπύλη συντονισμού
Μπορεί
να ακούγεται περίεργα, αλλά η αρχή της αβεβαιότητας αποτελεί εργαλείο
για τον ακριβή προσδιορισμό του πολύ μικρού χρόνου ζωής βαρέων
σωματιδίων που παράγονται σε συγκρούσεις υψηλής ενέργειας επιταχυντών. Η
σχέση αβεβαιότητας ενέργειας-χρόνου στη μορφή $\Delta E \cdot T \cong
\hbar/2 $, υποδηλώνει ότι για σωματίδια με εξαιρετικά μικρή διάρκεια
ζωής, θα υπάρχει σημαντική αβεβαιότητα στη μετρούμενη ενέργεια (μάζα).
Έτσι, για ένα σωματίδιο που έχει πεπερασμένη διάρκεια ζωής, η αρχή της
αβεβαιότητας θέτει ένα θεμελιώδες όριο στη γνώση της ενέργειάς του για
κάθε δεδομένη μέτρηση. Αυτό δεν σημαίνει ότι δεν μπορούμε να μετρήσουμε
την ενέργεια με πολύ μεγάλη ακρίβεια. Μπορούμε να το κάνουμε μετρώντας
την ενέργεια πολλές φορές και λαμβάνοντας την μέση τιμή.
Κι όταν
ανασυνθέσουμε την τιμή της μάζας (ενέργειας) του αρχικού ασταθούς
σωματιδίου, θα βρούμε μια κωδωνοειδή κατανομή πιθανοτήτων, που
ονομάζεται καμπύλη συντονισμού ή κατανομή Lorentzian ή Breit-Wigner:
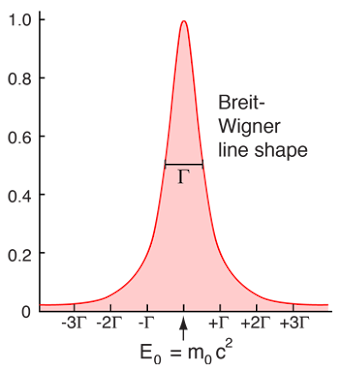 |
| Οι μετρήσεις της ενέργειας (E0) ενός ασταθούς σωματιδίου καθορίζουν μια κατανομή ενέργειας (natural line shape) που ονομάζεται Breit-Wigner ή Lorentzian |
Η κορυφή της καμπύλης αντιστοιχεί στην κεντρική τιμή της μάζας και όσο πιο σύντομη είναι η μέση διάρκεια ζωής του σωματιδίου, τόσο αυξάνεται το εύρος της. Κι εδώ κρύβεται το ιδιοφυές κόλπο.
Aν συμβολίσουμε με Γ το πλήρες πλάτος της κατανομής ενέργειας στο ήμισυ της μέγιστης τιμής της (FWHM=Full Width at Half Maximum),
η αβεβαιότητα στην ενέργεια εκφράζεται εύλογα ως $\Delta E = \Gamma/2 $
και η εξίσωση της αβεβαιότητας που συσχετίζει την μέση διάρκεια ζωής
σωματιδίου Τ με το εύρος Γ της κατανομής ενέργειας γράφεται ως $\Gamma \cdot T = \hbar $.
Αν μετρήσουμε το εύρος Γ της κατανομής, εύκολα υπολογίζουμε τον χρόνο ζωής Τ του σωματιδίου.
Το Γ αναφέρεται συχνά ως "φυσικό πλάτος γραμμής (natural line width)". Είναι ένα πολύ σημαντικό μέγεθος στη φυσική των επιταχυντών υψηλής ενέργειας και ο υπολογισμός του από την ανάλυση των πειραμαματικών δεδομένων προσδιορίζει, διαμέσου την σχέσης αβεβαιότητας (Γ∙Τ=h/2π), τους εξαιρετικά μικρούς χρόνους ζωής των παραγόμενων σωματιδίων.
Έτσι λοιπόν, η αρχή της αβεβαιότητας του Heisenberg , που φαίνεται να περιορίζει την ικανότητά μας να μετράμε, μετατρέπεται τελικά σε ένα κόλπο για να συλλάβουμε τους απειροελάχιστους χρόνους της ζωής ασταθών σωματιδίων.
Bιβλιογραφία:
1. "Μodern Physics from a to Z0" , James William Rohlf - John Wiley & Sons
2. "H προέλευση της μάζας", Γιάννης Ηλιόπουλος, ΠΕΚ
3. "Χρόνος (Από τον μύθο του Κρόνου στο CERN)", Guido Tonelli - εκδόσεις διόπτρα
4. Particle lifetimes from the uncertainty principle - http://hyperphysics.phy-astr.gsu.edu/hbase/quantum/parlif.html
